The past decade has seen so many incredible advances in astronomy that it would be hard to single out one as standing above the others. But near the top of my list is the work by Andrea Ghez (UCLA) and her colleagues to measure the mass of the Milky Way’s central black hole. In a paper posted on the Web last week, they derive a new and improved mass for our galaxy's monster in the middle.
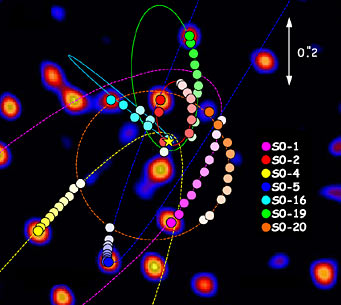
The orbits of stars within the Milky Way's central tenth of a light-year loop around the known location of the central black hole (yellow star symbol). The fuzzy blobs are diffraction-limited star images in an infrared adaptive-optics frame taken by a 10-meter Keck telescope in 2004. The frame is 1 arcsecond (0.13 light-year) square. While every star in this image has been seen to move, estimates of orbital parameters are only possible for those that show significant curvature so far.
The annual average positions for these stars are plotted as colored dots (which have increasing color saturation with time). Also plotted are the best-fitting orbit solutions. These orbits provide the clearest reading yet on the mass of the central black hole. Click for movie.
UCLA Galactic Center Group / Keck Observatory
The team’s pure measurement yields a mass of 4.1 million Suns with an uncertainty of only 0.6 million Suns. But if the black hole is assumed to be stationary with respect to the rest of the galaxy (and there's no evidence otherwise), its mass rises a bit to 4.5 million Suns with an uncertainty of only 0.4 million. This latter result is significantly higher than previous measurements made by Ghez’s team and by a European group led by Reinhard Genzel (Max Planck Institute for Extraterrestrial Physics, Germany).
A black hole of that mass has a diameter of 0.1 astronomical unit (about 9 million miles).
Why is this measurement so amazing? The center of the Milky Way is 27,000 light-years away, and it's hidden behind thick clouds of gas and dust along our line of sight. How do you measure the mass of an invisible object tens of thousands of light-years from Earth when even its surroundings are obscured from view?
Ghez and her team had to employ all the resources of modern astronomy: a really big telescope, detectors that operate in the infrared, and the relatively recent technology of adaptive optics (AO for short). Oh yeah, they also needed a lot of patience.

This narrow-field image of the galactic center, taken at an infrared wavelength of 3.8 microns, resolves many stars around the position of the central black hole ("Sgr A*). The frame is 10 arcseconds tall. Keck's Laser Guide Star adaptive-optics system achieved a resolution of 82 milliarcseconds here, the equivalent of resolving a pair of headlights in New York from Los Angeles.
Alan MacRobert
For the past decade, they have been observing the galactic center with the 10-meter Keck I and II telescopes in Hawaii. Keck gives them the brute-force light-gathering power to see stars in the galactic center. They observe at infrared wavelengths, which can penetrate the thick clouds of gas and dust. And most of all, they use AO, which involves a laser-generated artificial guide star and flexible, deformable mirrors to compensate for the rapid-fire blurring effects of Earth’s atmosphere.
The combination of these techniques allowed the group to resolve dozens of individual stars near the galactic center. Incredibly, the team could trace the curving orbital motions of several of these stars over more than a decade, and actually create a movie of these motions. Astronomers of just 25 years ago would have considered this magic.
The high mass of the Milky Way’s black hole, known as Sagittarius A* (pronounced "A-star"), made this possible. Anything orbiting near such a massive object is going to move really, really fast. These stars are whirling around the black hole at speeds exceeding 4,500 km per second (10 million miles per hour). One star in particular, dubbed S0-2, has been clocked at nearly 8,000 km/sec. By using simple orbital laws dating back to Isaac Newton in the 1600s, Ghez could use these stellar velocities to derive the mass of the central gravitating object.
In their new paper (accepted for publication in the Astrophysical Journal), Ghez and her team took into account various effects, such as uncertainties in star positions, ignored by in previous studies. “It’s been a bit like teenagers making emphatic but uninformed statements,” explains Ghez. “In our new paper, we try to take an honest look at where the problems are. We’ve learned that things are more complicated. We’re growing out of our teenage years!”
Besides coming up with a more precise mass measurement, the latest observations refine the distance to the Milky Way’s center: 27,400 light-years, with an uncertainty of 1,300 light-years.
In addition, the group finds no evidence that the central black hole is being gravitationally yanked around by the mass of another. This argues in favor of the team’s higher mass measurement. This new, higher mass value is also more consistent with predictions based on the famous relationship between black-hole mass and the total mass in the spherical component of large galaxies.
Here's the group's paper, their website, and
more imagery.
 3
3
Comments
William Vittitow
August 28, 2008 at 3:57 pm
I did not see in the article if they took doppler shift measurments. This would allow deriving how the orbits are inclined to the plane of the view. I assume they would do that if it is possible.
You must be logged in to post a comment.
Stephen John
August 30, 2008 at 1:20 am
Consider a black hole as a solution for Ric = 0, a spacetime that is, by definition, empty. Then no "outside bodies" are present by hypothesis. GR is non-linear, so the 'Principle of Superposition' does not apply. It does apply in Newton's theory. One cannot insert lumps of matter into any spacetime of GR by an analogy with Newton's theory. Thus black holes at the centres of galaxies are nonsense. So are black hole collisions, mergers and binaries. Each basic black hole is obtained separately as a solution to Ric = 0. The one black hole cannot therefore be in the spacetime of another black hole and mutually interact in a mutual spacetime that by definition contains no matter. Before one can talk of black hole interactions it must first be proved that the two-body problem is well-defined within GR. This can be done in only two ways, (a) derivation of an exact solution to the field equations for two bodies, or (b) proof of an existence theorem. There are no known solutions to the field equations for two or more bodies, so option (a) has never been fulfilled, and no existence theorem has ever been proven, so option (b) has never been fulfilled. General Relativity has not been able to account for the experimental fact that two fixed bodies will approach one another upon release.
SR forbids infinite density because infinite density implies that a material body can acquire the speed of light in vacuo. GR cannot violate SR, and so it too forbids infinite density, and hence forbids black holes. Nobody has ever found a black hole because nobody has ever found an infinitely dense singularity and nobody has ever found an event horizon. It takes an infinite amount of time for an observer to establish the presence of an event horizon, but nobody has been and nobody will be around for an infinite amount of time.
http://www.sjcrothers.plasmaresources.com/Unicorns.pdf
http://www.ptep-online.com/index_files/2007/PP-09-14.PDF
http://www.ptep-online.com/index_files/2008/PP-12-11.PDF
You must be logged in to post a comment.
arbizu
October 1, 2008 at 4:55 pm
I simply can´t believe that a scientific publication uses
miles still. I know the answer: In the USA that´s the
standard, so why not educate your readers and help them
out of the dark ages?
You must be logged in to post a comment.
You must be logged in to post a comment.