A new measurement, made using radio interferometry, argues that the distance to the Pleiades star cluster measured by ESA's Hipparcos satellite is decidedly wrong — and that ground-based astronomers had it right all along.

Akira Fujii
Last week I spent some blissful nights observing from rural Maine under pristine skies. In the wee hours I could see that familiar celestial landmark, the Pleiades star cluster, rising in the northeast over a stand of pine trees. They looked so delicate and serene — hardly the subject of a controversy that has nagged at astronomers for 1½ decades.
Open star clusters like the Pleiades and Hyades are perfect proving grounds for models of stellar evolution because their stars all have the same age and composition yet exhibit a wide range of masses. But for these models to work, it's critical that astronomers know the clusters' distances precisely.
Enter Hipparcos, a small orbiting observatory launched by the European Space Agency in 1989. Its name is both an acronym for High-Precision Parallax Collecting Satellite and a namesake for the ancient Greek astronomer/mathematician Hipparchus of Rhodes.
To gauge the distances of stars, Hipparcos used a technique already familiar to astronomers: trigonometric parallax. The spacecraft measured the position of roughly 120,000 nearby stars from various points along Earth's orbit to within about 0.001 arcsecond. Far more precise than possible with ground-based telescopes, these measurement sets revealed tiny shifts of nearby stars against the background of more distant ones. A star that's 1 parsec (3.26 light-years) away exhibits a positional shift of 1 arcsecond over a baseline of 1 astronomical unit (the mean Earth-Sun distance).
So, in principle, Hipparcos should have provided accurate parallaxes to stars up to many hundreds of light-years away, easily refining the distances to nearby open clusters such as the Pleiades (Messier 45) and Hyades clusters in Taurus, the Beehive (Messier 44) in Cancer, and the Alpha Persei Cluster.
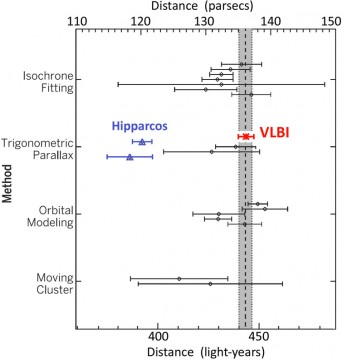
Eager astronomers jumped at the mission's results when released in 1997, but the "Pleiades problem" arose almost immediately. As detailed in a pair of articles here and here, ground-based methods had consistently shown that the Pleiades lie about 435 light-years (133 parsecs) away. However, according to Hipparcos, the cluster has a distance of just 392 light-years (120.2 parsecs), supposedly with an error of less than 1%.
If the cluster really was 10% closer than everyone had thought, then its stars must be intrinsically dimmer than stellar models suggested. A debate ensued about whether the models or the spacecraft data were wrong. Much hung in the balance, but the discrepancy remained unresolved. The Pleiades problem remained a major embarrassment among astrometrists worldwide.
A New and Better Yardstick
Carl Melis & others / Science
Now Carl Melis (University of California, San Diego) and others have seemingly put the matter to rest. In the August 29th issue of Science, they report distance results derived with a different and powerful method: very-long-baseline radio interferometry. They have seemingly nailed the distance at 444.0 light-years (136.2 parsecs), likewise accurate to within 1%.
The distance found by Melis's team agrees well with previous ground-based determinations — and not with Hipparcos. If this result holds up, it’s good news for the standard models of how stars work. But astronomers must try to understand why the Hipparcos observations misjudged the distance so obviously — and whether its entire database of stellar distances is suspect.
There's some suspicion that mission scientists failed to notice systematic positional errors during the processing of the Hipparcos data, but no one has yet turned up evidence for that. In any case, the mission team for Gaia, ESA's much more accurate follow-on astrometry mission, are taking special care.
In fact, as Léo Girardi (Padova Astronomical Observatory) points out in an accompanying Science perspective, by 2020 Gaia data should completely resolve any lingering aspects of the puzzling Hipparcos discrepancy. Perhaps there really were errors in the Pleiades distance determination — or, conceivably, the cluster's stars could be quite spread out along our line of sight.
Find the Pleiades and Hyades in Taurus, along with thousands of other stars and deep-sky objects, with Sky & Telescope's Pocket Sky Atlas.
 8
8
Comments
August 29, 2014 at 12:25 pm
For decades I have been bothered by the lack of discussion (and only obliquely mentioned in the last sentence) that the stars of the Pleiades are spread out over several parsecs and what effect that has had on this entire issue. With the Pleiades having an apparent diameter of ~2 degrees at a distance of 136 parsecs, its stars are spread out over ~5 parsecs in the plane of the sky. Assuming the cluster is roughly symmetrical, that would mean its stars would also have distances that vary on the order of 5 parsecs. Admittedly this is larger than the Hipparcos "anomaly" but it is bigger than the quoted measurement uncertainties.
You must be logged in to post a comment.
August 29, 2014 at 12:47 pm
No, it's smaller than the Hipparcos anomaly - 5 parsecs as against 13 (or even 16) parsecs.
You must be logged in to post a comment.
August 29, 2014 at 6:38 pm
Sorry, I meant to say that the distance span is smaller than the anomaly and therefore not its direct cause.
You must be logged in to post a comment.
Dean-Kennedy
August 30, 2014 at 2:06 pm
"positional shift of 1 arcsecond over a baseline of 1 astronomical unit"
Um, I have long been under the impression that the baseline was 2 astronomical units; that is, one full diameter of the earth's orbit, not just one radius. Is that incorrect?
You must be logged in to post a comment.
J. Kelly BeattyPost Author
September 1, 2014 at 11:56 am
hi, Dean... you'd think it'd be from one side of Earth's orbit to the other (2AU), right? but it's not: 1 parsec corresponds to a parallactic shift of 1 arcsecond over a baseline of 1 AU.
You must be logged in to post a comment.
Fred Shuman
September 5, 2014 at 12:15 am
As Kelly says, it's the 1-au radius of Earth's orbit, rather than the 2-au diameter, and that's so that everything works from the amplitude of the position-vs-time sine wave.
In electronics, this is called, the "center-to-peak" excursion of a waveform; the other is called, the "peak-to-peak" excursion.
You must be logged in to post a comment.
John-Murrell
December 5, 2016 at 6:07 am
In a recent lecture by Gerry Gilmore ( of Gaia) he stated that the Gaia results agree with the results from Steller modeling for the distance to the Pleiades. I have not seen a published paper on this yet. If the distance to the Pleiades is wrong it is not clear if there is an error in other Hipparcos measurements as well or is it a 'one off' ? A number of the ex-Hipparcos team are working on Gaia so they may be too busy to try to understand what may have gone wrong - assuming this is confirmed in a paper. The cause will need to be understood as it could impact the Gaia measurements as well as Gaia is really a more sensitive better version of Hipparcos but uses similar methods of measurement.
One interesting error graph on Gaia shows the tilt of one of the mirrors a sine wave which looked quite large till Gerry Gilmore pointed out the amlitude is equal to 1/10 diameter of a Helium atom !!
You must be logged in to post a comment.
Sempronio Vince
January 2, 2017 at 10:46 pm
I just ran a quick Gaia query with the following criteria:
RA/Dec: Simbad coordinates of M45
All stars within +/-5 parsecs of the above mentioned distance of 136 parsecs.
Here is the breakdown of stars by magnitude:
< M #
6 0 (Gaia isn't providing bright star info yet?)
7 6
8 15
9 27
10 43
11 61
12 74
13 75
14 75
Interesting. no additional stars dimmer than mag 13. I used the brightest 74.
so, the average the parallaxes of each of the 74 stars = 0.007411... or 134.92... parsecs
wow, that is a whole parsec closer than the published value.
Of course I'm not sure if the 74 stars are all members of the Pleiades, but the 5 parsec radius is double what the estimated size is and should have gotten a high percentage of them. If there were stragglers (non-members), then i would have expected to see some dimmer stars as well, but i also don't know if Gaia was measuring any dimmer in that area of the sky.
Crude estimate, but until i can understand all the data elements
You must be logged in to post a comment.
You must be logged in to post a comment.