Here's an update on an amateur astronomer's amazing effort to prove that Einstein really was right during the 2017 total solar eclipse.

Donald Bruns
As you've perhaps read in Sky & Telescope's August 2016 issue, I'm gearing up for an experiment during next year's total solar eclipse that will use off-the-shelf equipment and software to measure the deflection of starlight due to the Sun's gravity — and thus prove that Einstein's general theory of relativity really is correct!
Since I wrote that article, there's good news on my data analysis for the eclipse experiment: I have demonstrated that I can measure the deflection of stars in a twilight sky to 0.05 arcsecond. This result shows that the equipment I am using will work! My test came too late to include in the S&T article, but I'll be updating my forthcoming presentation at the SAS Symposium with the new results shown below.
Here is what I did:
On April 20th, just after the sun set at 7:25 p.m., I focused my Tele Vue NP101is refractor on Procyon and locked the focuser. I then slewed my Bisque Paramount MyT to the location of the "right" reference star field (indicated in the sky chart below) and waited 15 more minutes. At 7:45 p.m., the Sun had dropped to 6° below the horizon. This produces a twilight sky as bright as during a typical total eclipse.
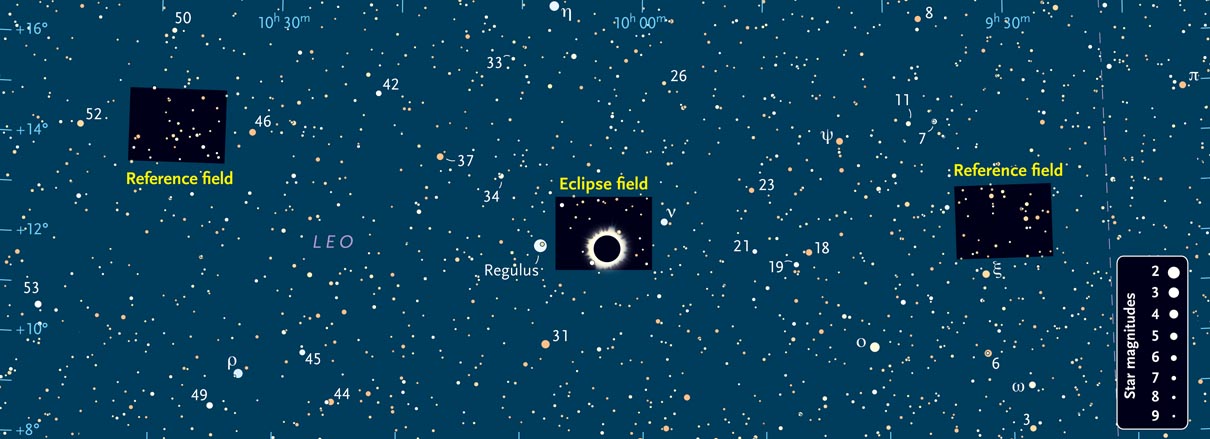
S&T: Leah Tiscione; source: Donald Bruns
I captured 7 frames on the Finger Lakes ML8051 camera, each 3 seconds long, and then immediately slewed 8° to the area where the Sun would be during the eclipse. I captured 25 frames there, each 1 second long. I then immediately slewed 8° on the other side to the "left" calibration field and captured 7 more frames in 30 seconds.
The total time to accomplish all this was 2 minutes 20 seconds, just as long as totality in Wyoming during the 2017 eclipse. This is a good dress rehearsal — all that was missing was the Sun’s gravity and the corona.
I processed the star centroids from all 39 images using MaximDL, Pinpoint, and Astrometrica. I was able to find 26 measurable stars in the eclipse images, and 36 and 42 good stars in the reference fields. I calculated the plate scale in the reference fields, and averaged them to get the plate scale to use in the eclipse field. This preliminary analysis can be considered as a “sanity check” on the entire experiment.
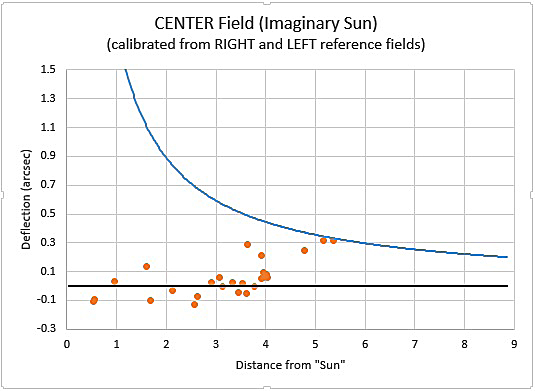
Donald Bruns
Then I plotted this data to show the deflection as a function of radial distance from the simulated Sun. Since there was no Sun, the gravitational deflection should be zero. The blue line in the graph at right is the deflection expected with the Sun in place in August 2017, and the orange dots are the deflections measured in April. The black line is the case for no gravity; as expected, the measured points cluster around this line.
For comparison, look at the data plot from a similar experiment, conducted in 1973, that had an 11% uncertainty. In that graph, shown below, the larger circles have the most confidence. Note that in the 1973 data, most of the stars are more than 4 solar radii away, while the stars in my plot are concentrated between 2 and 4 radii. This means that I will be measuring much larger deflections next year.
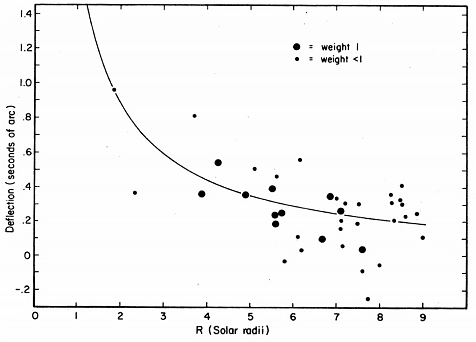
Donald Bruns
During the eclipse in 2017, I expect there will be fewer stars than in this “pretty good” simulation, but even if half of these stars are measurable, I think the results prove the capability of the equipment, my technique, and the data analysis.
The scatter in the data shows the measurement accuracy, and I'm working on a few improvements to reduce this scatter. The points toward the right side of my graph do not average to zero, for example. It turns out that these are stars near the edge of the camera frame. To simplify this preliminary data analysis, I did not include optical distortion, which (according to my zenith tests) is about 0.25 arcsecond — just about what is showing in the graph. Once I include this data correction, I am confident that those data points will also average to zero.
I will be making some other minor changes in the coming year to reduce the uncertainties even further. My final tests will be next spring, using the optimized configurations and updated software and procedures I am starting to write. I think my goal of measuring the deflection to the highest precision ever realized from the ground, using amateur equipment based on modern technology, is proven to be realistic.
If you want to learn more about my experiment, please read the detailed article that I prepared for the SAS Symposium. Also please contact me if you want to try to duplicate this project or offer help.
 7
7

Comments
Truth in this guy
July 21, 2017 at 5:06 pm
I want to know exactly how the stars were measured during the 1919 solar eclipse, that are used to prove the theory general of relativity (TGR). If gravitational lensing is really observable, how do we know it is due to the warping of spacetime?
If Einstein had prior knowledge of the lensing effect they saw in 1919, before he came up with his TGR then any measurable lensing wouldn't prove a thing, does it? Besides that the lensing is observable.
You must be logged in to post a comment.
Donald BrunsPost Author
July 21, 2017 at 5:34 pm
Einstein came up with his solar deflection idea after he came up with his theory of relativity. No one had seen any lensing effect in previous eclipses, partly because the deflections are so very small. It took several eclipse tests before the deflection data was good enough that most everyone agreed Einstein was right!
You must be logged in to post a comment.
Truth in this guy
July 28, 2017 at 9:42 pm
Thank you Donald,
It means a great deal to me, being able to exchange ideas with people in this field.
That is strange, I found information saying a German astronomer named Johann Georg von Soldner was the first to publish calculation of the deflection of light by mass in 1801. I found that info at Einstein online, here is the link.
http://www.einstein-online.info/spotlights/light_deflection
Yes, deflections are so very small indeed. Space.com says "the starlight is deflected by a minuscule amount (invisible to the naked eye)". Question is, were they really able to be measured in 1919. I believe it is something like measuring 1/3,600 of a degree.
Also, as far as I have found, the story goes, during the 1919 eclipse British astronomer Sir Arthur Eddington snapped some photos (which are questionable at best) studied them and declared Einstein was correct. The New York Times published the news on Nov. 7, 1919, and overnight Einstein was famous. But that is just what Space.com says.
Anyway, lately I've discovered or realized that the Sun, in addition to passing overhead, is in fact local. Have you paid attention to the Sun? Have you noticed it gets hotter when the sun is closer and colder when it is far away. It sure would be great to have more knowledgeable people like yourself onboard. There is very much we must uncover; so the time is ripe for regular people to make profound discoveries.
Thank you again, sincerely, Jeromey
You must be logged in to post a comment.
Truth in this guy
August 1, 2017 at 10:08 pm
As it turns out, there is evidence that Einstein did know about the lensing effect. That means TGR didn't predict the lensing, and Einstein was not correct. Back to the drawing board.
You must be logged in to post a comment.
Dean
August 6, 2017 at 4:33 am
From a scientist's point of view, prior knowledge of a phenomenon doesn't detract from studies of it. For example, obviously people were aware of the difference in the motions of planets and stars a thousand years before Kepler studied them. His achievement wasn't to declare that the planets move but to describe mathematically *how* they move. Prior to his work, nobody could accurately predict the position of a planet at some point in the future, but he gave us the math to do exactly that.
Same goes for the vast majority of science, we see a thing that seems odd and we don't know why it happens, so we study it. Whether you believe that space can be "stretched" and any of the other unintuitive claims of relativity (SR and GR) is, I think, beside the point of what you are alluding to.
Einstein didn't just say that light deflection occurs, he gave us the ability to quantify it. So it's not as if prior knowledge that is was a physical phenomenon really helped him in anyway.
As an aside, a better example is the precession of Mercury's orbit. With great hubris, physicists had the opinion in the late 1890s that they had everything worked out except for a few esoteric things like the fact that they could not predict Mercury's orbit with the same precision as all the other planets. Well, again, Einstein was surely aware of this but his goal was not to solve that dilemma. His work was substantially broader but the fact remains that once he completed his work on GR, it needed to be tested and so probably at that point he started looking for phenomenon that no other theory could explain quantitatively and many were found and still are being found.
One last example, GPS simply doesn't work *at all* without GR and I dare say he didn't have prior knowledge of that application 😉
You must be logged in to post a comment.
Dean
August 6, 2017 at 4:02 am
Donald,
I am gearing up to do the very same experiment. I saw your post last week but have just now had time to finish reading it. I'd love to share notes on the setup and execution. For now just a few comments/questions.
1. I see you are using a scope with very similar specs, ~f5 as well as a similar camera. My initial thoughts were that this setup would not provide enough accuracy considering the optical path converts to about 2"/px and that even at the sun's limb we are looking at only a 1.75" deflection. Obviously there are processing techniques that can help to isolate the exact pixel but still that's a lot of error.
2. The field stars I have selected range from 20.0'-25.6' radius from the sun center of mass which gives me a target deflection of 1.1" - 1.4" to try to measure. Is this about the range you are targeting?
3. I'm also worried about magnitude. I've been searching for some indication on coronal brightness but haven't found anything definitive. From what I can gather, the corona brightness will be at or higher than that of the best targets deflection-wise but there are at least two good stars. The main issue here is exposure time. Various eclipse photography sites recommend ~0.50s exposures for DSLRs @ low ISO to avoid overexposure from the corona. I think the well is higher on the astronomical cameras but not sure.
4. This comment is a real tangent but I bring it up as a curiosity... From a experimental point of view my goal is to obtain accurate enough results so as to give a definitive case for relativity. I'm reasonably well versed in cosmology so it's not like I have any doubt. To that end I've played devil's advocate armed with pre-GR science. At the time, say 1905, one could, naively by modern standards, make a reasonable argument that light deflection is predicted without using GR... (by 1905, Planck had published an energy eq for light but the question of photon mass was still unsettled). Now, the net of that is that if you use classical equations, you end up with a deflection but only half what GR predicts. So to truly prove GR is correct, one would have to show not only the existence of deflection centered on the GR expectation but that are also statistically distinct from a value of half the prediction. So I'm considering my f/10 C8 SCT (.5"/px)
You must be logged in to post a comment.
Esnuka
September 20, 2017 at 4:40 pm
The fact that gravity affects double to light does not need to imply anything about the geometry of space. Moreover, it does not fit in the lift experiment used to explain the Equivalence Principle of General Relativity. The Law of Global Gravity explains both gravitational lensing and Mercury's orbit precession.
https://molwick.com/en/gravitation/075-gravitational-lensing.html
You must be logged in to post a comment.
You must be logged in to post a comment.